The Design of Rijndael
基本概念
state: 状态矩阵,初始为输入明文/密文构成的矩阵,作为每一次轮变换的输入。
Nb: state矩阵的列数,Nb = 块长 / 32
cipher key: 输入的加密密钥
Nk: Nk = 块长 / 32
若矩阵的每个元素的长度为1Byte,则state和cipherkey分别为4 * Nb(Nk)的矩阵,其中每一列是一个块
### 算法流程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Rijndael (State, CipherKey) {
KeyExpansion(CipherKey, ExpandedKey); //密钥扩展
AddRoundKey(State, ExpandedKey[0]); //轮密钥加
for (i = 1; i < Nr; i++) Round(State, ExpandedKey[i]); //轮变换
FinalRound(State, ExpandedKey[Nr]);
}
Round(State, ExpandedKey[i]) {
SubBytes(State);
ShiftRows(State);
MixColumns(State);
AddRoundKey(State, ExpandedKey[i]);
}
FinalRound(State, ExpandedKey[Nr]);
1. SubBytes
SubBytes是加密算法中唯一的非线性变换。对于输入矩阵中的每个元素,直接通过查表得到对应的替换元素。输入参数为4 * Nb列的矩阵state和S盒。代码如下:
1
2
3
4
5
6
void SubBytes(word8 state[4][MAXBC], word8 box[256]) {
int i, j;
for (i = 0; i < 4; i++)
for (j = 0; j < Nb; j++)
state[i][j] = box[state[i][j]];
}
解密时,SubBytes的逆变换即为将box换为S盒的逆矩阵Si.
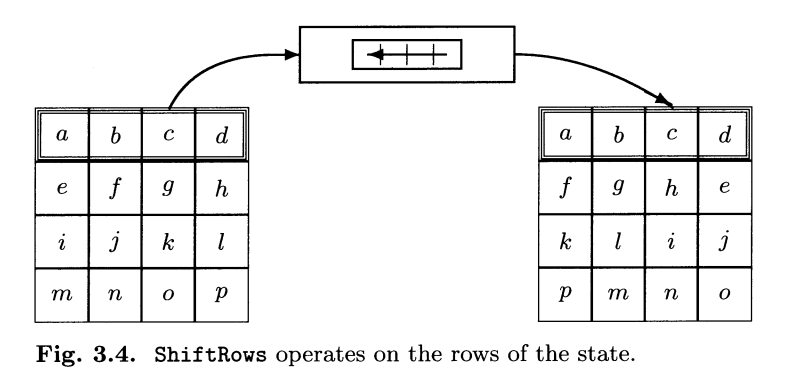
2. ShiftRows
ShiftRows对于矩阵的每一行进行不同长度的移位。移位的长度与Nb直接相关。移位的示意图如下:
当加密时,矩阵依次左移C0,C1,C2,C3位。当解密时,依次左移Nb-C1, Nb-C2, Nb-C3位。
代码如下,输入为状态矩阵state和标志位d,当d为0时表示为加密,当d为1时表示为解密:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void ShiftRows(word8 state[4][MAXBC], word8 d) {
word8 tmp[MAXBC];
int i, j;
if (d == 0) {
for (i = 0; i < Nb; ++i) {
for (j = 0; j < Nb; j++)
tmp[j] = state[i][(j + shifts[Nb - 4][i]) % Nb];
for (j = 0; j < Nb; j++)
state[i][j] = tmp[j];
}
}
else {
for (i = 1; i < 4; ++i) {
for (j = 0; j < Nb; j++)
tmp[j] = state[i][(Nb + j - shifts[Nb - 4][i]) % Nb];
for (j = 0; j < Nb; j++) state[i][j] = tmp[j];
}
}
}
3.MixColumns
MixColumns以线性方式进行矩阵的列混合,即让状态矩阵成为一个特定的矩阵与它自身的乘积。
加密时,对于矩阵的每一列,有
其中b为置换后的矩阵,a为置换前的矩阵。运算在GF(256)中进行,对应元素之间的乘积可以通过查表ALogtable和Logtable来完成,加法实质上为异或。则MixColumns的算法实现为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void MixColumns(word8 state[4][MAXBC]) {
word8 tmp[4][MAXBC];
int i, j;
for (j = 0; j < Nb; ++j)
for (i = 0; i < 4; i++)
tmp[i][j] = mul(2, state[i][j])
^ mul(3, state[(i + 1) % 4][j])
^ state[(i + 2) % 4][j]
^ state[(i + 3) % 4][j];
for (i = 0; i < 4; i++)
for (j = 0; j < Nb; j++)
state[i][j] = tmp[i][j];
}
word8 mul (word8 a, word8 b) {
if (a && b) return Alogtable[(Logtable[a] + Logtable[b]) % 255];
else return 0;
}
MixColumns的逆过程InvMixColumns的实现仅所乘矩阵不同,其他操作相同,代码如下:
void InvMixColumns(word8 state[4][MAXBC]) {
int i, j;
word8 tmp[4][MAXBC];
for (j = 0; j < Nb; j++)
for (i = 0; i < 4; i++)
tmp[i][j] = mul(0xe, state[i][j])
^ mul(0xb, state[(i + 1) % 4][j])
^ mul(0xd, state[(i + 2) % 4][j])
^ mul(0x9, state[(i + 3) % 4][j]);
for (i = 0; i < 4; i++)
for (j = 0; j < Nb; j++)
state[i][j] = tmp[i][j];
}
4. KeyAddition
state与ExpandedKey[i]对应项相异或,代码如下:
1
2
3
4
5
6
void AddRoundKey(word8 state[4][MAXBC], word8 rk[4][MAXBC]) {
int i, j;
for (i = 0; i < 4; ++i)
for (j = 0; j < Nb; j++)
state[i][j] ^= rk[i][j];
}
5.KeyExpansion
KeyExpansion是AES中代码最复杂的一部分,扩展密钥ExpandedKey的规模由Nb和Nk确定,ExpandedKey定义为MAXROUNDS+1 * 4 * MAXBC的三维矩阵。那么在第i轮轮密钥加时,ExpandedKey[i]就是需要需要使用的4 * MAXBC的扩展密钥矩阵。
扩展密钥的前Nk列由输入密钥直接填充,而第i列的密钥分为两种情况:
- 如果i是Nk的倍数,那么第i列是第i - Nk列与i - 1列的按位异或
- 如果不是,那么第i列是第i - Nk列与i - 1列的非线性函数的按位异或,这个非线性函数是S盒+一个循环常量。
- 特殊情况:如果Nk >= 6,那么当i % Nk ==4 时,与上面第二种情况相同。
在计算轮密钥时,按照每块为4 * Nk列来计算,在进行轮密钥加时,按照每块4 * Nb列来划分。代码及注释如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
int KeyExpansion(word8 key[4][MAXKC], word8 ExpandedKey[MAXROUNDS + 1][4][MAXBC]) {
int i, j, t, RCpointer = 1;
word8 tk[4][MAXKC];
/*
* the first Nk columns are filled with the cipher key.
*/
for (j = 0; j < Nk; j++)
for (i = 0; i < 4; i++)
tk[i][j] = key[i][j];
t = 0;
/* copy values into round key array*/
for (j = 0; (j < Nk) && (t < (ROUNDS + 1) * Nb); j++, t++)
for (i = 0; i < 4; i++)
ExpandedKey[t / Nb][i][t % Nb] = tk[i][j];
/*
* tk中存放的是column i - 1的密钥
* 如果i不是Nk的倍数,那么第i列是第i - Nk列和第 i - 1列的按位异或, 否则第i列是第i - Nk和第 i - 1列的非线性函数的按列异或
*/
while (t < (ROUNDS + 1) * Nb) {
// tk 4 * Nk的矩阵 每一列与他的后一列异或,
/*
* 第 0 列 与 i - 1列的S盒置换异或
*/
for (i = 0; i < 4; i++)
tk[i][0] ^= S[tk[(i + 1) % 4][Nk - 1]];
tk[0][0] ^=RC[RCpointer++];
/*
* 当KC <= 6时, 只有第0列是Nk的倍数,剩余的第1 到KC-1列只需要与第j - 1列异或
* 当KC > 6时, 第 0 列和第3列需要与S盒进行异或,其他的需要与j-1列进行异或
* Nk = keylength / 32, Nb = blocklength/32
* 计算轮密钥时,按照Nk * 4来计算,划分时按照每组4 * Nb依次存放
*/
if (Nk <= 6)
for (j = 1; j < Nk; j++)
for (i = 0; i < 4; i++)
tk[i][j] ^= tk[i][j - 1];
else {
for(j = 1; j < 4; j++)
for (i = 0; i < 4; i++)
tk[i][j] ^= tk[i][j - 1];
for(i = 0; i < 4; i++)
tk[i][4] ^= S[tk[i][3]];
for(j = 5; j < Nk; j++)
for(i = 0; i < 4; i++)
tk[i][j] ^= tk[i][j - 1];
}
/* copy values into round key array */
for (j = 0; (j < Nk) && (t < (ROUNDS + 1) * Nb); j++, t++)
for (i = 0; i < 4; i++)
ExpandedKey[t / Nb][i][t % Nb] = tk[i][j];
}
return 0;
}
#### 6. Encrypt & Decrypt
加密即为上述几种基本操作的组合,Decrypt为几种逆运算的组合,代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
int Encrypt(word8 state[4][MAXBC], word8 rk[MAXROUNDS + 1][4][MAXBC]) {
/*
* Encryption of one block
*/
int r;
/* key addition */
AddRoundKey(state, rk[0]);
for (r = 1; r < ROUNDS; r++) {
SubBytes(state, S);
ShiftRows(state, 0);
MixColumns(state);
AddRoundKey(state, rk[r]);
}
/*
* final round don't have MixColumns
*/
SubBytes(state, S);
ShiftRows(state, 0);
AddRoundKey(state, rk[ROUNDS]);
return 0;
}
int Decrypt(word8 state[4][MAXBC], word8 rk[MAXROUNDS + 1][4][MAXBC]) {
int r;
AddRoundKey(state, rk[ROUNDS]);
SubBytes(state, Si);
ShiftRows(state, 1);
for (r = ROUNDS-1; r > 0; r--) {
AddRoundKey(state, rk[r]);
InvMixColumns(state);
SubBytes(state, Si);
ShiftRows(state, 1);
}
AddRoundKey(state, rk[0]);
return 0;
}